Torus Networks Tasarım

Torus ağları, en iyi performans gösteren süper bilgisayarlarda sıklıkla kullanılır. Bazı dezavantajları vardır, ancak ana faydaları - maliyetleri - onları çok büyük kurulumlar için uygun hale getirir. Ayrıca, bazı hesaplama algoritmalarında, hesaplama düğümleri esas olarak en yakın komşularıyla veri alışverişinde bulunur ve bu durumda torus topolojisi algoritma ile güzel bir şekilde çakışır.

Bu sayfada, torus ağlarının nasıl yapıldığının açıklamasını (örnek bir kablo düzeni dahil) ve torus (ve yağ ağacı) ağlarını otomatik olarak tasarlamaya izin veren web servisine bir bağlantı bulacaksınız.

Yeni başlayanlar için kağıt katlama egzersizleri

Torus (çoğul "tori") çöreğe benzeyen bir şekildir. Nasıl oluyor da bu terim bilgisayar ağları için kullanılıyor?

Bu örneğe bir göz atalım. Dikdörtgen bir kağıt alın ve üzerine bir ızgara çizin. İletişim kurmak istediğiniz bilgisayarları bu kılavuzun kesişimlerine yerleştirin. Izgara çizgileri iletişim bağlantılarınızı temsil edecektir. Gördüğünüz gibi, sol üst köşedeki bir bilgisayar, sol alt köşedeki arkadaşına kolayca ulaşamaz: paketin tüm ızgara boyunca dibine doğru ilerlemesi gerekir.

Ancak, doğrudan alttaki bilgisayara giden başka bir iletişim bağlantısı ekleyebilirsiniz. Izgaranızdaki diğer tüm bağlantılardan daha uzun olacak gibi görünebilir, ancak kağıdınızı boru şeklinde katlamayı deneyin, böylece sayfanızın üst ve alt kenarları hizalanır ve yukarıda belirtilen iki bilgisayarın artık çok yakın olduğunu göreceksiniz (kısa bir iplikle iki kenar diktiğinizi hayal edin, bu sizin yeni bağlantınız olacak).

Bu bağlantı, birbirlerinden çok uzakta olan bilgisayarlar için iletişim gecikmesini büyük ölçüde azaltır. Ancak bu tek bağlantı, kağıdınızın "başka bir ucuna" giden paketler için zaman kazandırsa da, hızla aşırı kullanılacaktır. Bu nedenle, işleri daha iyi hale getirmek için, üst sıradaki her bilgisayardan alt satırdaki eşine kadar iki kenarı birbirine bağlamak için birden fazla bağlantı ekleyebilirsiniz.

Şimdi, ipliği (varsa) çıkarın, kağıdınızı açın ve masaya geri koyun. Sol üst köşedeki aynı bilgisayarı düşünün, ancak şimdi sağ üst köşedeki bilgisayarla iletişim kurmak istiyor. Yine, "normal" bir hareket, paketin kağıdın üst kenarı boyunca takip etmesini gerektirir. Peki ya sayfanızı tekrar boru şeklinde katlarsanız, bu sefer sol ve sağ kenarları hizalarsanız? İki bilgisayar yine çok yakındır ve bunları doğrudan bağlamak için bir bağlantı ekleyebilirsiniz. Ve önceki durumda olduğu gibi, daha iyi bir bant genişliği elde etmek için, kağıdınızın sol kenarından sağ kenarına giden birçok bağlantı ekleyebilirsiniz.

Her şeyi geri açın ve bir dakika düşünün. Her iki optimizasyonu da aynı anda yapabilir ve sayfayı aynı anda her iki yönde katlayabilir misiniz? Cevap evet, biraz sezgisel olsa da, çünkü kağıt bunu göstermek için en iyi araç değil. Kauçuk gibi iyi esneyen bir şeye ihtiyacımız olacak. İlk adım, sayfanızdan bir tüp yapmaktır. Ardından, tüpün her iki ucunu da bağlamanız gerekir ve bu, germenin gerekli olduğu yerdir. Sonuç... bir torus — bu ağların adı da buradan geliyor! Wikipedia'dan bu animasyona bir göz atın; Bu şaşırtıcı:

Dikdörtgenden Torus. Wikipedia kullanıcısı Kieff tarafından animasyon. Kaynak: Wikipedia Commons.

2D torus bu şekilde yapılır. Gerçek hayatta, bilgi işlem donanımınızı dev bir çöreğin köşelerine dağıtmanıza gerek yoktur. Bunun yerine, diğer ağlarda olduğu gibi, bilgi işlem odanızın zeminindeki raflarda bulunur. Ve uzaktaki bilgisayarlara ulaşmanız gerektiğinde daha uzun kablolar kullanılır, tıpkı kağıt sayfanızın iki kenarını bir tüpe katlamadan birleştirmeye çalıştığınızda daha uzun bir dişe ihtiyaç duyacağınız gibi. (Aşağıdaki örnekte olası bir kablo düzenine göz atacağız).

3D torus nasıl yapılır?

Hala kağıt alıştırmalarından bıkmadınız mı? Düz kağıt maketinizdeki uzun sarma bağlantıları için pamuk iplikleri kullandığınızı varsayalım. Bu çok düzgün görünmeyecek, ama umurumuzda değil. İki boyutunuzun her birinde kaç bilgisayarınız var? Yatay bir boyutta N ve ayrıca dikey bir boyutta N olduğunu varsayalım. Unutmayın: ideal bir torus ağı, her boyut boyunca aynı sayıda düğüm kullanan ağdır, aksi takdirde ağ dengesiz hale gelir. 2D torusunuz (bir masanın üzerinde düz durmasına rağmen) NxN hesaplama düğümlerini birbirine bağlar.

Şimdi, N benzer kağıt maketleri yapın ve hepsini masanızın üzerine bir yığın halinde yerleştirin. Sol üst köşeden başlayın. Bunları hesaplama düğümü boyunca tablonun yüzeyine dik olarak dikin ve iğne yığından arkadan çıktığında, hesaplama düğümleri arasında bir "boş alan" kullanarak yığını tekrar ters yönde delin, böylece ipliği başladığı düğüme getirin. Ardından, tüm NxN düğümleri için aynısını yapın. 3D torus bu şekilde yapılır. NxNxN düğümlerini bağlayabilir. N=10 ise, 10x10x10=1000 düğüm bağlayabilirsiniz. Bu oldukça büyük bir işlem kümesi!

Umarım bu alıştırmayı pratikte yapmazsınız, çünkü bir 3D torusu görselleştirmenin daha iyi yolları vardır. Şimdiye kadar karşılaştığım en iyi görüntülerden biri, Fujitsu'nun 2012'de K Computer için kullanılacağını düşündükleri ağı göstermek için yaptığı render'dır (ancak K Computer, Fujitsu'nun dediği gibi çok daha karmaşık bir "6D ağ / torus ağı" kullandı - videoyu buradan izleyin).

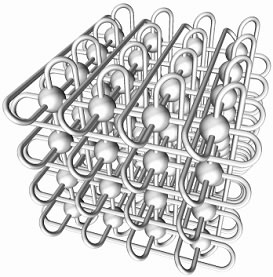
Fujitsu tarafından oluşturulan 3D torus. (c) Fujitsu ve RIKEN, 2009. Kaynak: basın açıklaması.

Gördüğünüz gibi, bir 3B torusta her hesaplama düğümü altı komşuya bağlıdır. Ve torusun "kenarında" bulunan düğümler hala 6 komşuya bağlı, sadece uzun sarma bağlantıları kullanıyorlar.

Bir torusta daha fazla boyut için ana motivasyon, çok sayıda düğümü bağlarken düşük gecikme süresini korumaktır. Örneğin, N=1000 düğümü 2B torus ile bağlamak istiyorsanız, 32×32 ızgaraya ihtiyacınız olacaktır. Bilgisayarlar rastgele bir şekilde veri alışverişi yapıyorsa, paketin hedefine ulaşmak için böyle bir ızgara üzerinde kat etmesi gereken ortalama mesafe, 10×10×10 küple elde edilebilecek mesafeden daha büyüktür. Izgaranın sol üst köşesinden, en uzak hedef onun merkezindedir. 32×32'lik bir ızgarada, ızgaranın merkezine ulaşmak için kabaca sağa 16 adım atmanız ve ardından aşağıya doğru 16 adım atmanız gerekir - bu toplamda 32 adımdır.

10×10×10'luk bir küple, bir tepe noktasından merkeze ulaşmak için, kenar boyunca bir yönde 5 adım, dik yönde 5 adım, küpün yüzünün bir merkezine ulaşmak ve son olarak küpün içine 5 adım atmanız gerekir - bu, önceki durumda 32'ye kıyasla sadece 15 adımdır. Daha fazla adım, daha büyük gecikme süreleri anlamına gelir ve bu da paralel hesaplamalar için çok zararlıdır. Bu nedenle büyük süper bilgisayarlar 5D (IBM Sequoia gibi) veya 6D tori kullanır.

Anahtarları kullanmak mı yoksa kullanmamak mı?

Bilgisayar endüstrisinde torus ağları oluşturmak için iki yaklaşım vardır. İlk yaklaşım, hesaplama düğümlerini torusunuzun "kafesine" yerleştirir. Bilgi işlem düğümlerinin ağ bağdaştırıcılarının içindeki devre, daha sonra ağ üzerinden akan paketleri iletmekle ilgilenir. Özel anahtarlara gerek yoktur (bunun nedeni, her ağ bağdaştırıcısının kendi başına küçük bir anahtar olmasıdır). Bu tür ağlara "doğrudan ağlar" denir, çünkü bilgi işlem düğümleri aralarında herhangi bir anahtar olmadan doğrudan birbirine bağlanır.

2D (iki boyutlu) torus ağları için, düğümünüzü dört komşuya bağlayan dört bağlantı noktasına sahip bir ağ adaptörüne ihtiyacınız vardır. Daha büyük 3D ağlar için altı komşu vardır, bu nedenle altı bağlantı noktasına sahip bir ağ adaptörüne ihtiyacınız vardır. Bu teknolojiye örnek olarak (1) Dolphin tarafından üretilen SCI adaptörleri (bu eski bir teknolojidir) ve (2) Prof. Dr. Ulrich Brüning'in araştırma grubu tarafından tasarlanan ve EXTOLL GmbH tarafından pazarlanan EXTOLL adaptörleri (çok yeni bir teknoloji) verilebilir.

Bu yaklaşımın önemli bir yararı, ağın anahtarlama elemanlarının, aktarılacak verilerin kaynaklandığı yere, yani CPU'ya mümkün olduğunca yaklaştırılabilmesidir. EXTOLL teknolojisi ile ağ adaptörleri, anakart üzerindeki bir HTX yuvası aracılığıyla bir HyperTransport veri yoluna takılır.

Ancak dezavantajları da var. Altı bağlantı noktasına sahip bir ağ bağdaştırıcınız varsa, bu, her bilgi işlem düğümüne altı kablonun bağlanacağı anlamına gelir. Kablo konektörleri yer kaplar (ve bunları küçültmek zordur), bu nedenle minyatürleştirme eğilimleri ile altı kablo belki de emtia donanımı için mevcut teknolojik sınırdır.

Rafa monte edilen her sıradan sunucuya bir bakır InfiniBand kablosu bağlamak bile hava akışını engelleyebilecek bir kablolama yapısı oluşturur. Altı kablo çok fazla. Teselli edici olan, bu altı kablodan ikisinin çok kısa bir mesafeye (yani söz konusu düğümün hemen üstündeki ve altındaki komşu hesaplama düğümlerine - gideceği gerçeğidir, böylece kalan dördünden biraz daha ince yapılabilirler. Veya ince ama maliyetli optik kablolar kullanabilirsiniz.

Neyse ki, torus ağları oluşturmak için başka bir yaklaşım daha var ve kalın kablo demetlerini bilgi işlem düğümlerine yönlendirmenizi gerektirmiyor. Bilgi işlem düğümlerini torusunuzun "kafesine" yerleştirmek yerine, ağ anahtarlarını oraya yerleştirebilirsiniz. Bu sıradan ağ anahtarları, örneğin 36 bağlantı noktalı InfiniBand anahtarları. Hesaplama düğümlerinin daha sonra sıradan ağ bağdaştırıcılarına sahip olması gerekir ve paket iletme anahtarlar tarafından yapılır. Bu tür ağlara "dolaylı" denir, çünkü hesaplama düğümleri birbirine doğrudan değil, anahtarlar aracılığıyla bağlanır.

Bunun belirli gecikme etkileri vardır, çünkü torus ağına ulaşmak için paketin ağ bağdaştırıcısından ve ardından anahtardan geçmesi gerekirken, önceki senaryoda yalnızca bir cihaz vardı - aynı zamanda bir anahtar görevi gören ağ bağdaştırıcısı - iki yerine. Aynısı alıcı taraf için de geçerlidir. Bu nedenle, uygulamalarınız için gecikme süresi önemliyse, karşılaştırmalara başvurmak ve size doğru gecikme süresi ve maliyet dengesini sağlayacak teknolojiyi seçmek isteyebilirsiniz. (Ve her ne pahasına olursa olsun en düşük gecikme süresi elde edilecekse, neden eski yağ ağaçlarını denemiyorsunuz? Ama ben dalıyorum...)

Bir bilgi işlem düğümünden bir anahtara yalnızca bir kablonun geçmesi gerekir - ancak bilgi işlem düğümünüz daha fazla bant genişliğine ihtiyaç duyuyorsa daha fazlasına sahip olabilirsiniz. Bu şekilde, 18 düğümü 36 bağlantı noktalı bir anahtara bağlayabilirsiniz. Anahtarın kalan 18 portu, komşularına - bir 3D torus ağında, 6'sına - her komşu anahtara üç kablo demeti bağlanacak. Mellanox Technologies'den Todd Wilde'ın insideHPC.com'dan Rich Brueckner tarafından filme alınan bu sunumuna bir göz atın veya slaytları HPC Danışma Konseyi web sitesinden PDF olarak edinin.

Kablo düzenine bir örnek

Hewlett-Packard blade sunucularla yapılmış bir bilgisayar kümesini ele alalım ve bunun için bir torus ağı tasarlayalım. Hewlett-Packard tarafından üretilen blade sunucular, içine hangi bileşenleri koyduğunuza bağlı olarak fiyatlarında büyük farklılıklar gösterebilir. Ancak, kullanmak istediğiniz belirli bir sunucu modelini (örneğin HP BL465c G8) ve yapılandırmasını belirlediğinizi ve bütçenizin 180 blade sunucu satın almanıza izin verdiğini varsayalım (bu arada, kabaca 2 milyon ABD doları olan en iyi performans gösteren CPU'larla). Blade sunucuları HP BladeSystem c7000 kasasına (kasa olarak da adlandırılır) yerleştirirsiniz ve her kasada 16 sunucu bulunur. Bu nedenle, 180/16=11,25=12 şasiye ihtiyacınız var.

Kasanın arka tarafında, bir InfiniBand anahtarı ekleyebileceğiniz bir ara bağlantı yuvası vardır. 32 bağlantı noktasına sahiptir. Bunlardan 16 bağlantı noktası, anahtarı taktığınız anda blade sunuculardaki ağ bağdaştırıcılarına elektriksel olarak bağlanır. Bu bağlantı türü, rafa monte sunucular için kablo kullanmaktan çok daha güvenilirdir. Anahtarın kalan 16 bağlantı noktası kullanıcı tarafından görülebilir ve kabloları diğer anahtarlara yaptığınız gibi bunlara bağlayabilirsiniz. 12 kasamız var, bu da 12 anahtar anlamına geliyor. 3×4 boyutlarında bir 2D torus ağı kuracağız (çünkü 6×2 torus dengesizdir ve daha da fazlası dejenere torus olan 12×1 halkası).

2D ağda, her anahtarın dört komşusu vardır. Bu nedenle, bir anahtarın 16 bağlantı noktası eşit olarak dağıtılacaktır - 4 komşunun her birine 4 bağlantı noktası - ve komşulara giden kablolar dörtlü demetler halinde çalışacaktır.

Tek bir kasa 10U alır, bu nedenle standart bir 42U rafa dört kasa yerleştirebiliriz. Burada çok şanslıyız, çünkü torusumuz 3×4 (veya 4×3, önemli değil) ve bir rafta dört kasayı torusun bir boyutu olarak kullanabiliriz (buna "y" boyutu diyeceğiz, çünkü bir raftaki kasalar dikey olarak istiflenir). Üç raf, "x" olarak adlandıracağımız başka bir boyut sağlar, çünkü raflar yatay eksen boyunca birbirine bitişiktir. Bu nedenle, topolojimizi "3×4" olarak adlandıralım.

Todd'un sunumunda verilen tavsiyeyi kullanacağız ve anahtar adları ve bağlantı noktaları için bir model seçeceğiz (sunumun 13. slaytı). Bağlantı noktaları ve raflarda yaptığımız gibi anahtarları '0'dan değil, yalnızca '1'den saymaya başlamayı seçtim. x ve y olmak üzere iki boyut olacak ve her anahtarın 16 portu dört gruba ayrılacak:

+y: 1, 2, 3, 4
-y: 5, 6, 7, 8
+x: 9, 10, 11, 12
-x: 13, 14, 15, 16

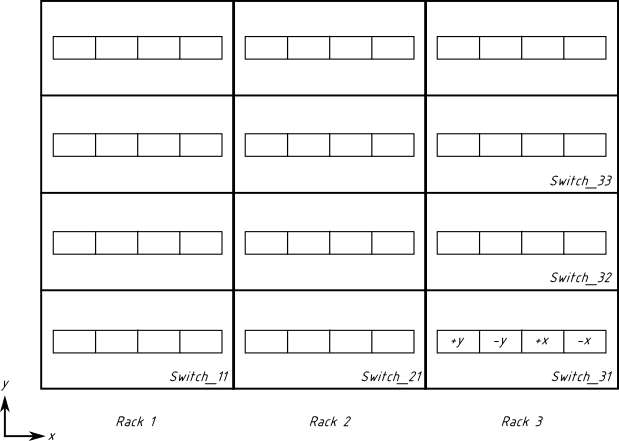
Aşağıda üç rafımızın grafiksel gösterimi bulunmaktadır (arkadan görünüm). Her rafta 4 kasa bulunur. Her kasanın bir anahtarı vardır. Her anahtarın 16 bağlantı noktası dört gruba ayrılmıştır (ayrıntılar için Switch_31 bakın). Çizim ölçeklendirilmez (gerçek 42U raflar gösterilenden daha yüksektir).

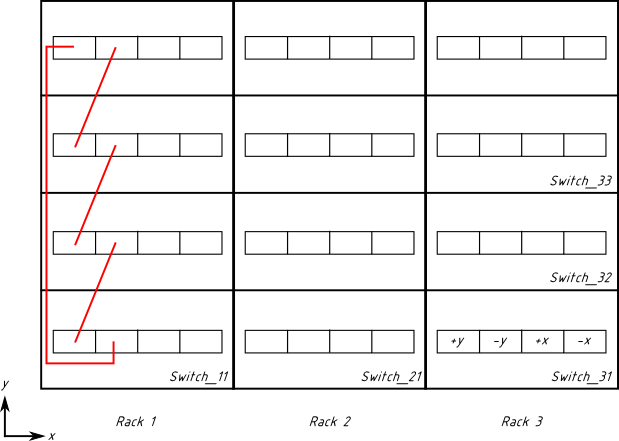
Kablolamaya y boyutunda başlayalım, çünkü daha basit. İleri gittiğimizde (y artar), "+y" grubundaki anahtar portlarını kullanırız. Kablolar "+y" grubundan sırayla bir sonraki anahtara, "-y" grubuna gider. İşte torusumuzun ilk halkası:

Kabloların "+y" → "-y" düzeninde olduğunu doğrulayın, örneğin Switch_11'daki "+y" grubundan Switch_12'daki "-y" grubuna. Özellikle iyi olan şey, bu kablolamanın tamamen rafın içinde olmasıdır. Baş üstü tepsisine veya diğer raflara gitmez. Her üç rafta da bağımsızdır. Bunu diğer raflarda da benzer şekilde yapıyoruz:

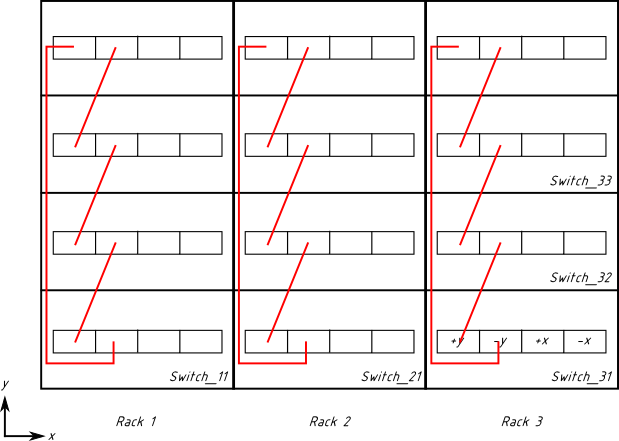
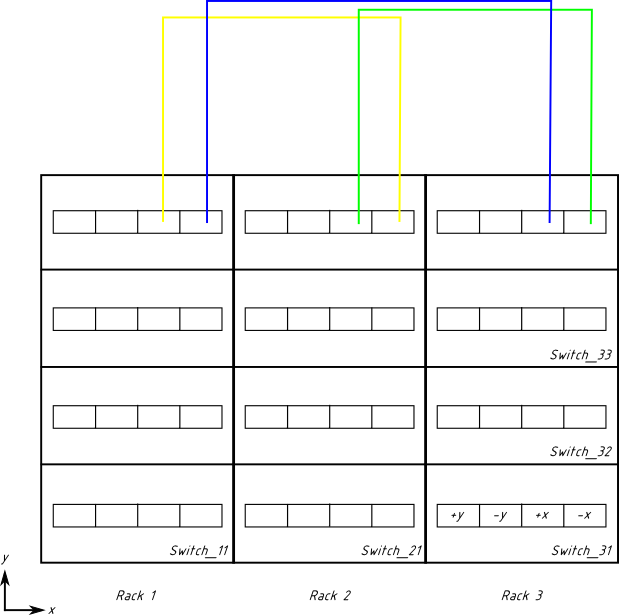
Şimdi, "y" boyutuyla işimiz bitti. "x" boyutu ile devam edelim. Zorluk, bu sefer kabloların bir raftan diğerine gitmesi gerektiğidir ve onları Switch_11'den Switch_21'ye çekerseniz, rafın kapıları kapanmaz, bu nedenle baş üstü tepsisini kullanmamız gerekir. Bu, özellikle rafın altında bulunan kasa için önemli ölçüde daha uzun kablolar gerektirir. Üst anahtarlarla başlayalım.

Kabloların sırası sarı, yeşil, mavidir. Kablolamanın "+x" → "-x" modelini izlediğini doğrulayın (yani, sarı kablo bir anahtarda "+x"ten bir sonrakinde "-x"e gider).

Ayrıca, kabloların şematik olarak düz yukarı çıkacak şekilde gösterildiğini, oysa gerçek hava soğutmalı kurulumda, hava akışını engellememeleri için bunları rafın yan tarafıyla hizalamayı seçeceğinizi unutmayın. Ve muhtemelen bu amaç için rafın sağ tarafını seçersiniz, çünkü sol taraf muhtemelen kablolarımız tarafından "y" boyutunda kullanılacaktır (gösterilmemiştir, ancak yine de oradadır).

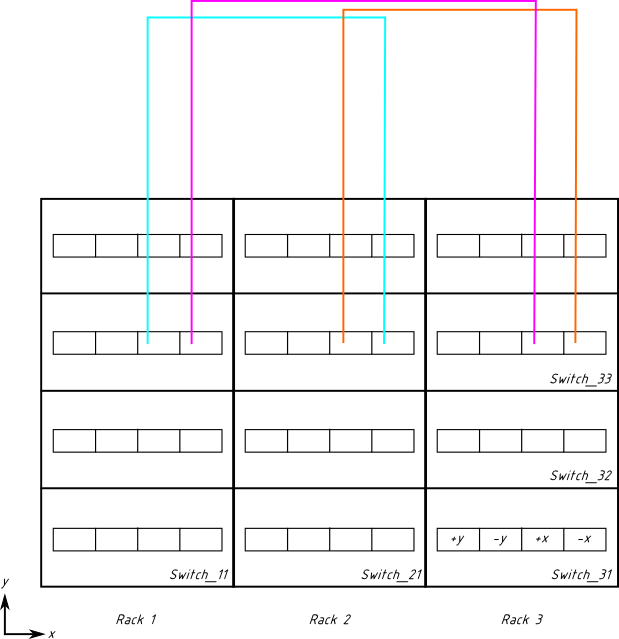
Bir sonraki anahtar sırası benzer şekilde kablolanmıştır (önceki kablolama görüntüyü karıştırmamak için gösterilmemiştir):

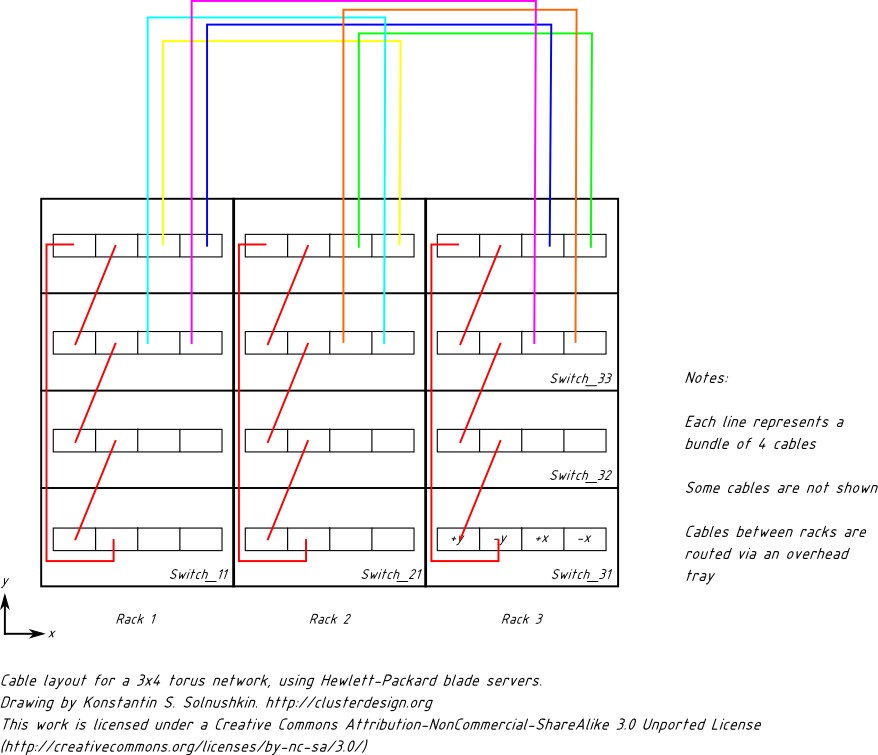
Şimdi iki alt anahtar sırasını benzer şekilde bağlamanız gerekiyor ve işiniz bitti. Önceki bölümlerde yapılan tüm kablolamayı tasvir etmeye çalışırsak, şöyle görünecektir:

Tebrikler! 180 düğüm için başarıyla bir 2D torus ağı tasarladınız. (Çizimi denemek isterseniz, en iyi Inkscape ile açılan SVG dosyasını indirmekten çekinmeyin).

Torus ağları doğal olarak yağ ağaçlarından daha ucuzdur. Gerçekten de, 12 bıçaklı şasi için bir yağ ağacı tasarlamaya çalışırsak, şasideki anahtarlar kenar anahtarları olarak işlev görür ve yağ ağacının ikinci seviyesi için ayrı bir çekirdek anahtar setine ihtiyacımız olur. Bu nedenle, yağ ağacı daha pahalı olacaktır. Aynı zamanda, düşük gecikme süresi ve engellemesiz bant genişliği sağlar. (Aslında, hesaplama düğümlerinin maliyetini hesaba katarsanız, yağ ağacı o kadar pahalı görünmüyor).

Torus ağlarının genişletilmesi

Yağ ağaçları, çekirdek seviyelerini en baştan doğru bir şekilde tasarlarsanız kolayca genişletilebilir. Peki ya tori — onları nasıl genişletebiliriz? Geleneksel yaklaşım, onları boyutlarından biri boyunca germektir.

Yukarıdaki örnekle, kablolamayı olduğu gibi "y" boyutunda bırakabilir (kırmızı kablolar, her rafta bağımsız) ve "x" boyutunda esneyebiliriz. Gerektiği kadar raf eklerdik ve eski ve yeni rafların kenarında, etrafı saran uzun bağlantıların (yukarıdaki şekillerde mavi ve mor) Raf 1'e geri dönmeyeceğinden, bunun yerine Raf 4'e devam edeceğinden emin olurduk. Sonunda, son Raf N'den, Raf 1'e geri dönen bir sarma bağlantısı olacaktır.

Raf N'den Raf 1'e sarma bağlantısı endişe verici derecede uzuyorsa, yukarıda belirtilen sunumun 13. slaytındaki kablolama tarifini kullanın. Bu şekilde, tüm kablolar biraz daha uzun olacak, ancak hiçbiri son derece uzun olmayacak.

Torus genişlemesinin bu geleneksel yolu dengesiz ağlara yol açabilir. 100×4 torusu nasıl bulursunuz? Böyle bir yapının işlevsel olabilmesi için yerine getirilmesi gereken iki koşul vardır:

1. Hesaplama kodunuz iletişimin yerelliğini göstermelidir. Aksi takdirde, bir hesaplama düğümünden diğerine giden paketlerin tüm aracı anahtarlardan geçmesi gerekir. Bu anahtarlar zaten diğer görevlerle meşguldür (bant genişliğini azaltır) ve bu anahtarların çoğu vardır (bu da gecikmeyi artırır).

2. Diğer koşulun yerine getirilmesi daha da zordur: iş planlayıcınız topolojiye duyarlı olmalıdır, böylece bir işin tüm süreçlerini torusun aynı bölümünde planlar (aslında, bu koşul dengeli tori için bile gereklidir). Torus topolojilerini açıkça destekleyen iş zamanlayıcıları biliyorsanız, lütfen bir yorum bırakın. (Kasım 2012'den itibaren güncelleme: MPI uygulaması olan MVAPICH2 artık topolojiye duyarlıdır).

Uzun lafın kısası, 100×4'lük bir torus inşa edemezsiniz ve bunun işe yaramasını umamazsınız. Onu diğer boyut(lar)da da esnetmeniz gerekir. Yukarıdaki örnekle, 100×4 yerine 20×20 torus yapabilirsiniz. (7x7x8=392 boyutlarında bir 3D torus daha da iyi olurdu, ancak her şeyi yeniden kablolamanız gerekecek).

Dikey boyutumuz — "y" — 4'e eşitti ve şimdi 20 olmasını istiyoruz. Şekillerimizin üzerinde "y" ölçüsü kırmızı kablolarla kablolanmıştır. Normalde 4 şasiye yayılır, bu yüzden 4'e eşittir. 20'ye eşit olmasını istiyorsak, 20 şasiye, yani 5 rafa yayılmamız gerekir. Kablolamayı daha basit hale getirmek için, orijinal sıramızın arkasına başka bir raf sırası eklememiz ve ardından bir tane daha eklememiz gerekir ve 5 sıramız olana kadar bu şekilde devam eder.

Şimdi, kırmızı kabloları yeniden bağlayın: ön sıradaki raftaki üst kasadan, ikinci raf sırasına gitmeli, o raftaki tüm kasalardan geçmeli, üçüncü sırayı takip etmeli ve beş sıranın tümü kucaklanana kadar bu şekilde devam etmelidir - ve sonra ön sıraya geri dönün.

Kulağa karmaşık mı geliyor? Evet, öyle, ancak gelecekteki genişlemenin doğru planlanması işleri kolaylaştıracaktır. Ayrıca, HPC kurulumları nadiren iki kattan fazla genişletilir, bu nedenle tek bir boyutta esneme amaçlarınız için yeterli olabilir.

Torus ağlarının otomatik tasarımı

Hızlı bir şekilde bir torus ağı tasarlamanız gerekiyorsa, bu sayfanın alt kısmında bağlantısı verilen web servisini kullanabilirsiniz. Yağ ağacı ve torus ağları tasarlayabilir, size ağ maliyeti, güç tüketimi ve diğer ölçümlerin yanı sıra satın almanız gereken ürün faturası hakkında hızlı tahminler sunar. Araç, sizin için uygun sayıda torus boyutunu otomatik olarak seçecektir.

Sonuç

1. Emtia InfiniBand donanımını kullanarak, HPC kurulumları ve genel olarak veri merkezleri için kolayca torus topolojileri oluşturabilirsiniz!
2. Ağ anahtarları, tüm yönlendirme karmaşıklığını halleder. Anahtar ve kablo arızaları otomatik olarak ele alınır.
3. Torus topolojileri, aynı sayıda hesaplama düğümü için yağ ağaçlarından daha ucuzdur. Ancak, hesaplama düğümlerinin maliyetini hesaba katarsanız, fiyat farkı azalır.
4. Gelecekteki genişleme mümkündür, ancak önceden planlama gerektirir.

kaynak

Torus Networks Tasarım | ClusterDesign.org